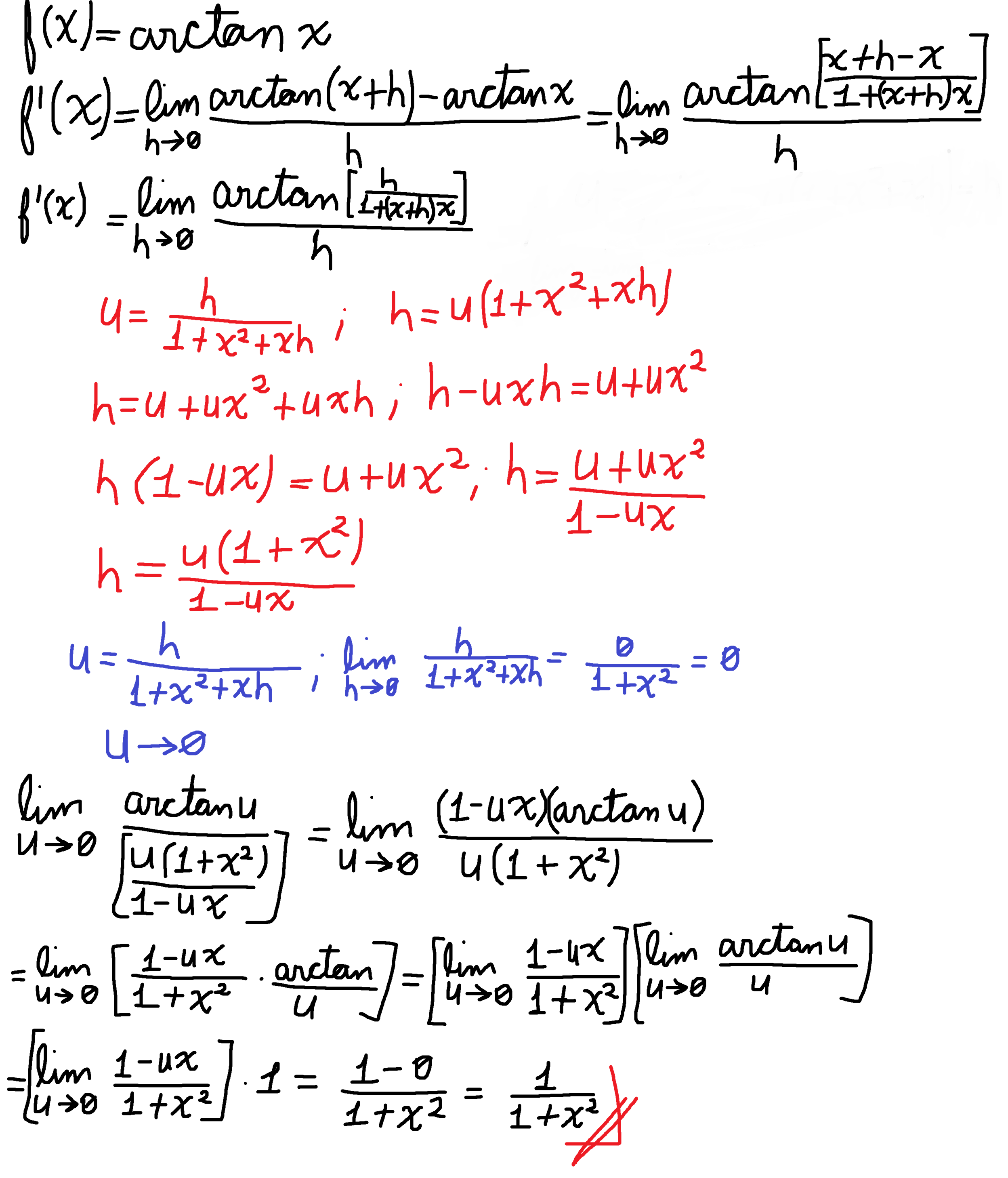
Derivative of arctan(x)

Ok then! This is going to be the first thing I'm going to put in here. So let's start with something relatively easy :-). We're going to derive the inverse tangent of x, or the arctangent of x. I certainly prefer to use notations as arctan(x) or atan(x) rather than (tan^-1)(x) to avoid confusions between cotangent and arctangent, as people could (rightfully!) think that tangent to the minus 1 power is simply cotangent! But that's a whole other issue and not really important right now. At the bottom, you have the whole problem solved without too much chitchattering, but rather disorganized. Although I can do worst, believe me ;-).

I'm going to use a substitution to resolve the indetermination. You can easily check that there is going to be a 0/0 indetermination. I've seen a couple of ways to resolve it. One is dividing by 1+(x+h)x and then multiplying by the same expression; that's not bad, but seems rather unnatural (to me, that is!) and it's not something a student would think right off the bat. Other way would trying to calculate the implicit differentiation of tangent, and it would be a implicit definition through a limit of k approaching zero of [k / [tan(x+h)-tan(x)]]. That's an interesting way of doing so, but the substitution way I'm currently showing you it's not regularly done (I haven't seen it anywhere else to be honest, so if you can say me who has done it first I'll gladly reference it). So let's begin with it!

First off, let's start with the 'tools'. You have to know the following notable limits, and trigonometric identities. They're not a whole lot:

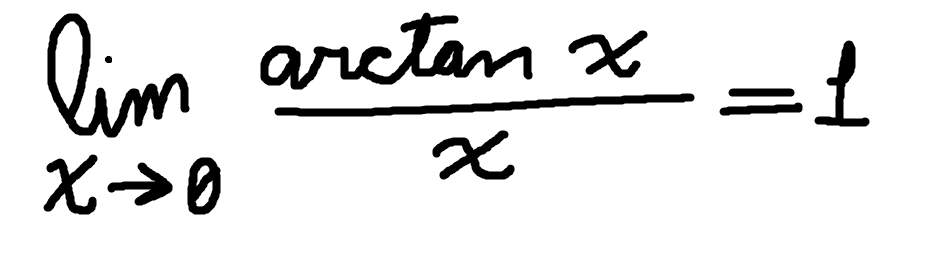
arc notable limit: the limit as x approaches 0 of arctan of x, then divided by x, is equal to 1

This limit is rather easy to prove (with a bit of help that is), so... why not, why shouldn't I prove it?

proof of the limit as x approaches zero of arctan of x, divided by x

Obviously, as you can (maybe) see I had to use the limit as x approaches zero of [tan(x)/x] without proving it, but that would be rather laborious. Then, the other tool we're going to use is:

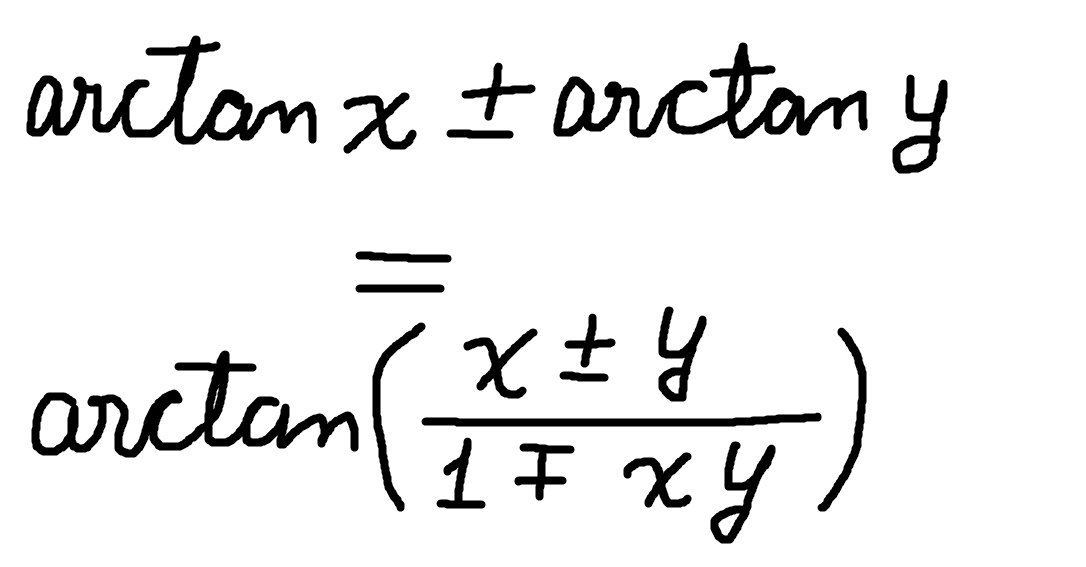
inverse trigonometric identity: the sum or difference of arctangents is equal to arctangent of the sum or difference of the tangent, divided by 1 minus if sum or plus if difference of x times y

This we're not going to prove either. Too much drawings to do so, and as you can see from (the) paint(ings), we'd rather not see my drawings :-).

Now, we have all we are going to need to calculate the derivative through the limit. Let's start!

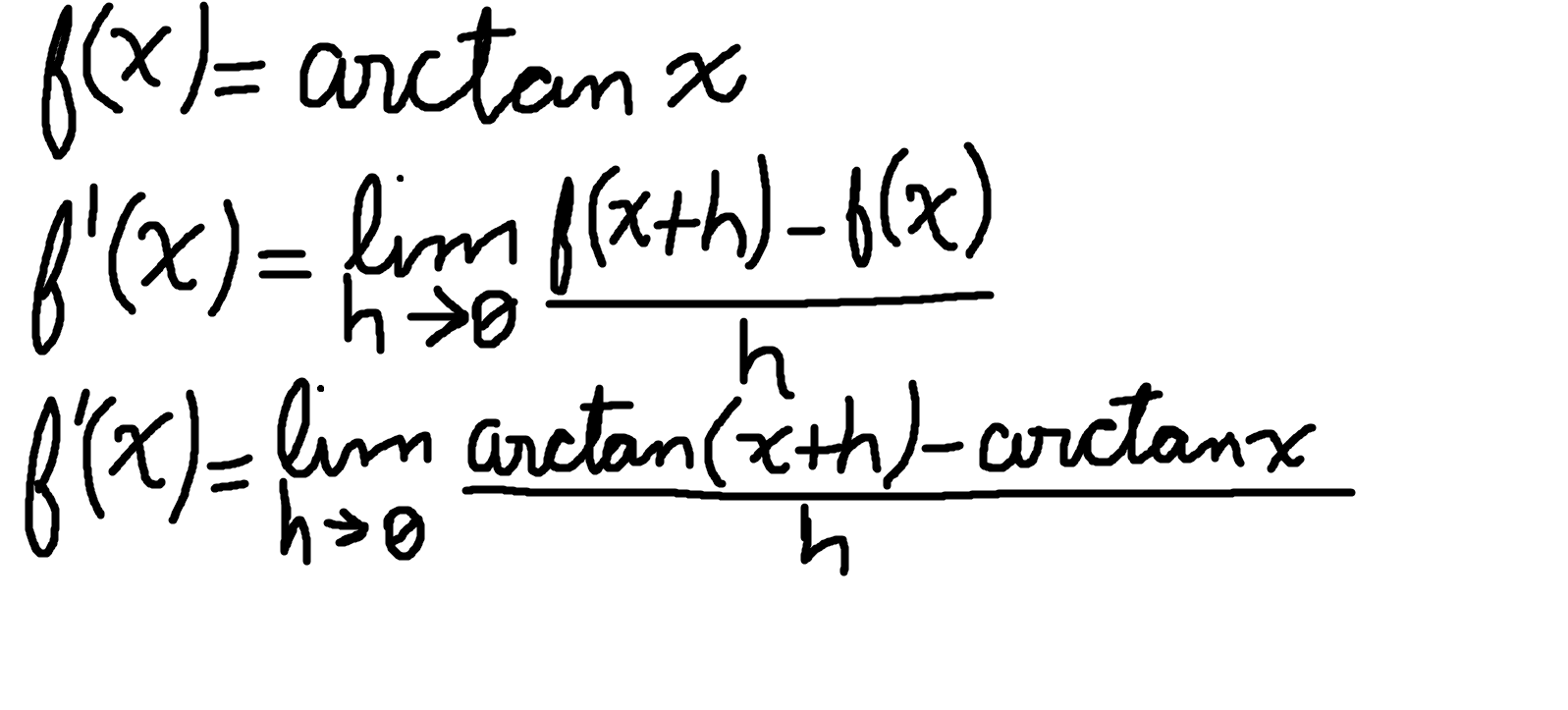
definition of the derivation of arctan(x), being: limit as h approaches zero of arctan of x plus h, minus arctan of x, divided by h

This is rather easy to see. If you're here, you should already know this, and I shouldn't have written that much :-P. But whatever, there's nothing bad about going back to the basics. As you can see, I prefer to use h rather than delta-x, but again, if you're here, you should be familiarized with that (at least a bit). It's a simple definition, the most used I'd even say. So let's develope it a bit!

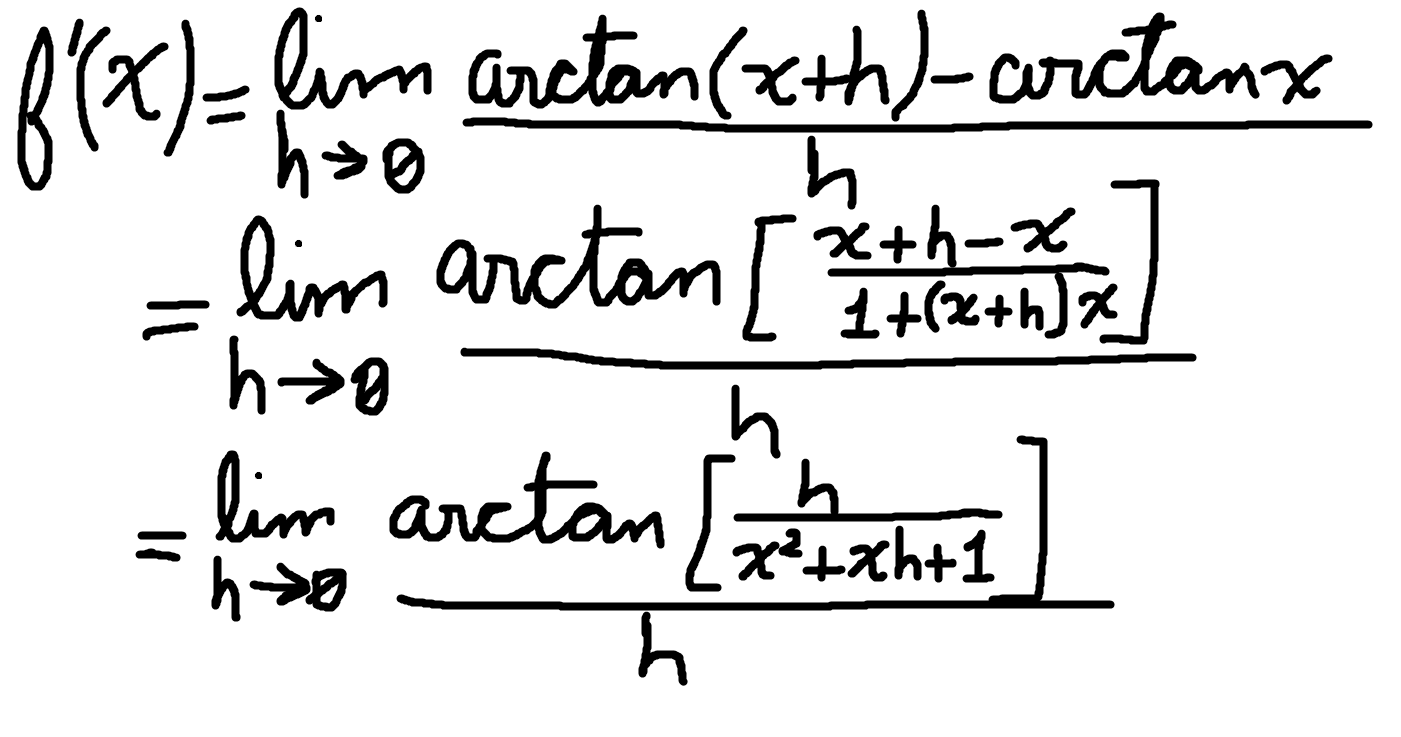
developing the definition, rather difficult to express to be honest

You can see we've already used our trigonometric identity! So that's good. The next step after this is rather complicated. Mathematicians like to solve this quickly and just divide and multiply by 1+(x+h)x in the denominator and then apply the arctangent limit we saw above. And there's nothing wrong with it, but I'd say I prefer using substitution because that's the way I'd see it if I ever did this without have never done it before. I-it's not as if I just did this the day before writing this, h-haha. We're going to say 'u' is equal to the tangent in the arctangent, and then we're going to use algebra to solve the equation for h.

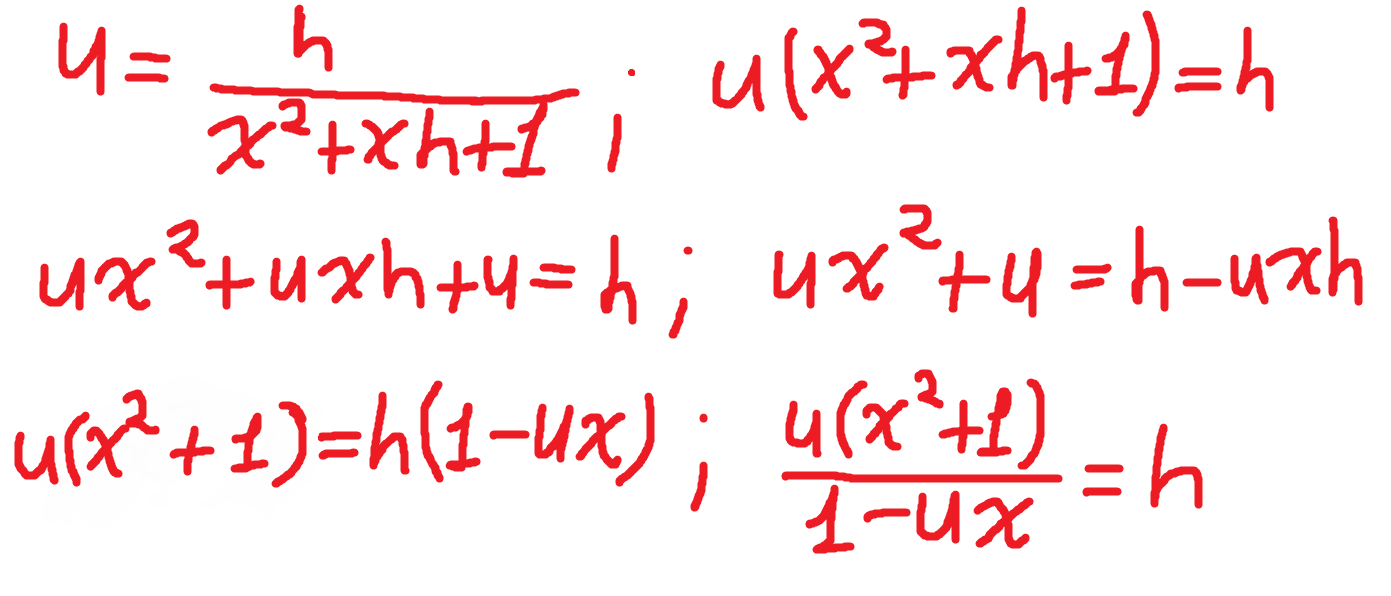
establishing parameter u that equals h divided by x squared plus x times h plus 1

Now we have defined our u and our h. But we have to know what approaches u if h is approaching zero. It's rather easy to see, but let's do it anyways.

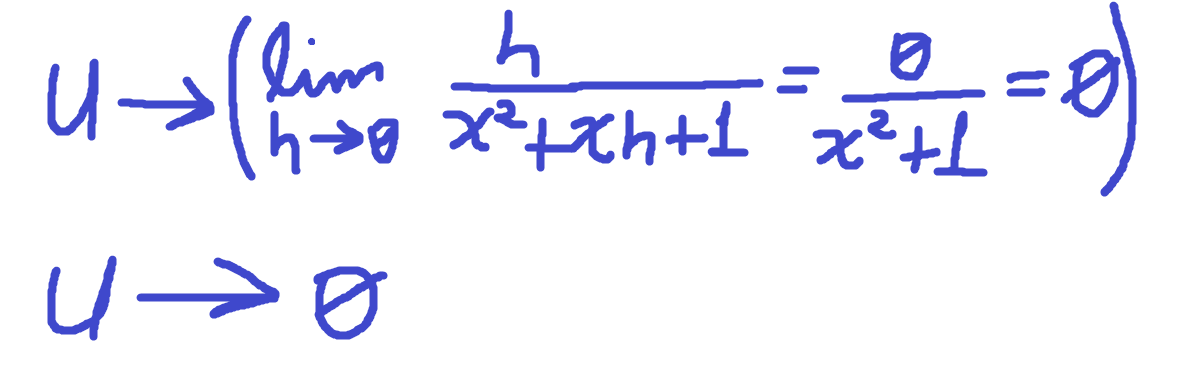
as h approaches zero, u approaches zero after calculating the limit of h approaching zero

Rather easy after all of this. Not very "automatic", of course, but it's better to go slow but steady than doing stuff quick and bad! Substitution is a very powerful thing, as you can see. And if you're a Calculus 1 student, get accustomed to using it and be comfortable with it. You're going to need it ;-). Then, let's substitute our u in the equation.

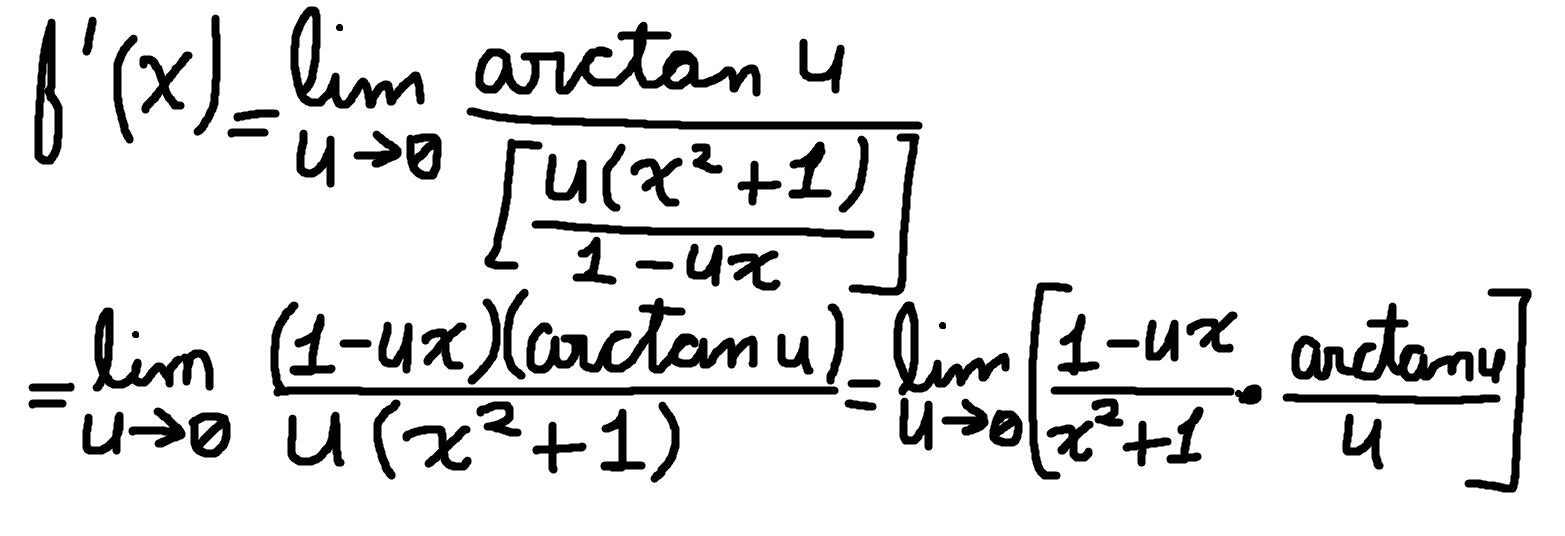
There's nothing weird being done, maybe just the substitution. The most perceptive ones would easily realise that this thing is already solved. But I'm going to solve it, anyways. Let's separate the expression through the limit of a product rule, and then solve it using notable limits (the one we prove it before) and simple substitution.

solving the limit using notable limits and substitution

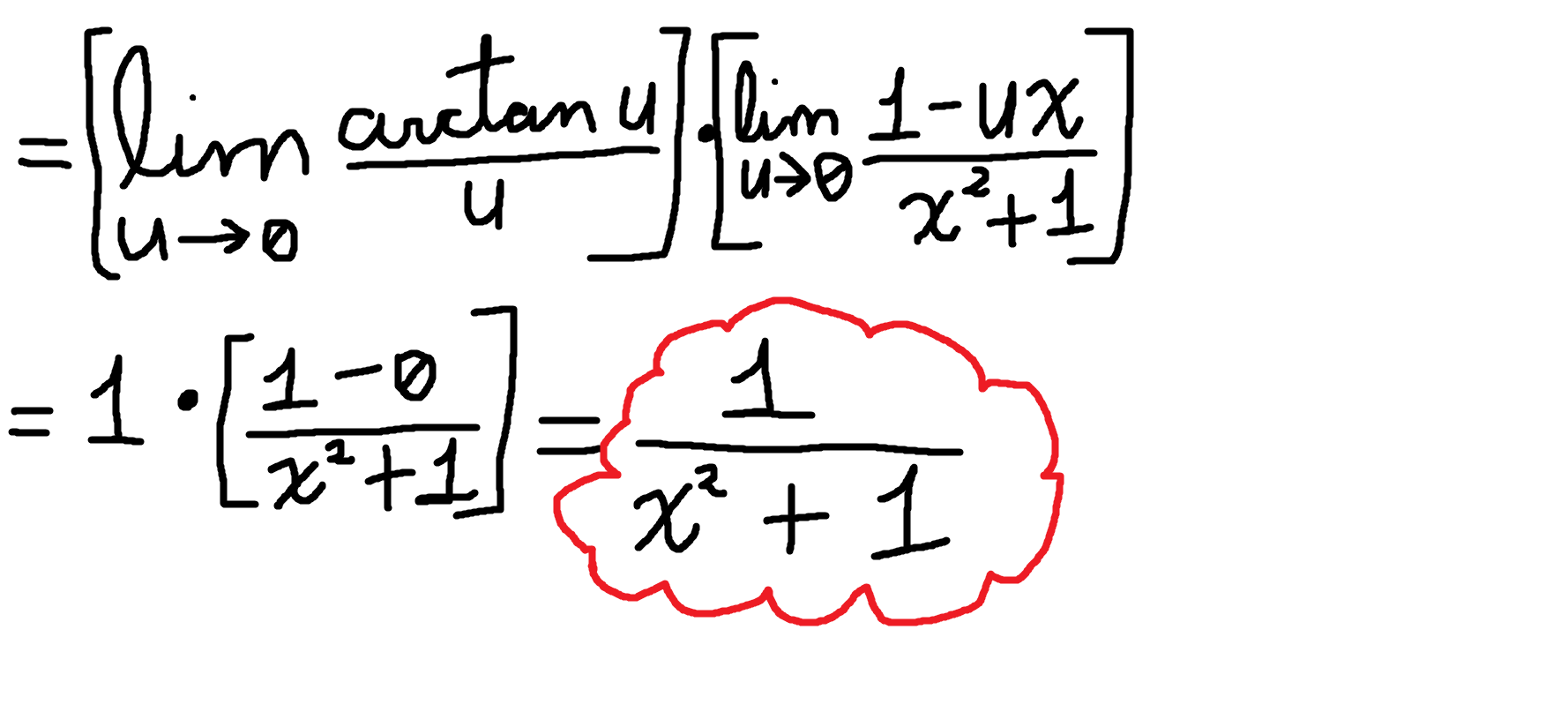
Aaand we're done! If you use normal rules of derivation, you would easily see that this is the correct answer of the derivative of the arctangent of x. Inverse trigonometric functions are very tricky, aren't they? If you have any comments or think I fucked up somewhere, please let me know! :-)